ESTIMACIÓN DE LIMITES MEDIANTE GRÁFICAS

ESTIMACIÓN DE LIMITES MEDIANTE GRÁFICAS

-LÍMITES UNILATERALES A PARTIR DE GRÁFICAS

En esta lección o unidad del tema de limites ,se tratara de construir la habilidad para visualizar límites al estimarlos por medio de las gráficas de las funciones. en esta primera parte examinaremos o analizaremos límites unilaterales y con la ayuda de este video sera mas facial entender como interpretar gráficos ya que se muestra en el la explicación de como hallar un limite unilateral por medio de gráficas 

a continuación se mostrara diversos ejercicios sobre la respectiva unidad que fueron desarrollados durante el periodo actual de clase.

- 1) a continuación mostramos la gráfica de la función F 

¿cual es el valor limite de F(x) conforme x se acerca a 3 por la derecha?

R//=lim x tiende a 3 por la derecha es = ∞

- 2) a continuación mostramos la gráfica de la función F 

¿cual es el valor limite de F(x) conforme x se acerca a -2 por la izquierda?

¿cual es el valor limite de F(x) conforme x se acerca a 7 por la derecha?

R//=lim x tiende a -2 por la izquierda es = 4

R//=lim x tiende a 7 por la derecha  es = 2

- 3) a continuación mostramos la gráfica de la función F 

¿cual es el valor limite de F(x) conforme x se acerca a 9 por la izquierda?

¿cual es el valor limite de F(x) conforme x se acerca a -6 por la izquierda?

R//=lim x tiende a 9 por la izquierda es = 0

R//=lim x tiende a -6 por la izquierda es = 4

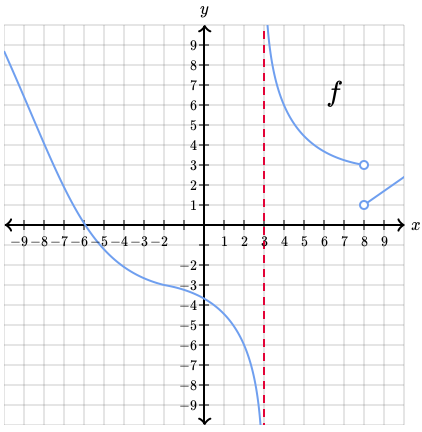
- 4) a continuación mostramos la gráfica de la función F 

¿cual es el valor limite de F(x) conforme x se acerca a 2 por la derecha?

¿cual es el valor limite de F(x) conforme x se acerca a -3 por la derecha?

R//=lim x tiende a 2 por la derecha  es = -4

R//=lim x tiende a -3 por la derecha  es = 3

R//=lim x tiende a -4 por la derecha  es =  ∞

- 5) a continuación mostramos la gráfica de la función F 

¿cual es el valor limite de F(x) conforme x se acerca a -4 por la izquierda?

¿cual es el valor limite de F(x) conforme x se acerca a -2 por la izquierda?

¿cual es el valor limite de F(x) conforme x se acerca a 9 por la izquierda?

R//=lim x tiende a -4 por la izquierda  es = 4

R//=lim x tiende a -2 por la izquierda  es = 8

R//=lim x tiende a 9 por la izquierda  es = -3

-LÍMITES BILATERALES A PARTIR DE GRÁFICAS

En esta lección o unidad del tema de limites ,se tratara de construir la habilidad para visualizar límites al estimarlos por medio de las gráficas de las funciones. en esta segunda parte examinaremos o analizaremos límites bilaterales  y con la ayuda de este video sera mas facial entender como interpretar gráficos ya que se muestra en el la explicación de como hallar un limite bilateral por medio de gráficas 

a continuación se mostrara diversos ejercicios sobre la respectiva unidad que fueron desarrollados durante el periodo actual de clase.

- 1) La gráfica de la función $f$ se muestra a continuación. ¿Cuál parece ser el valor de  

​x→−6​lim​​           f(x) ?

-La gráfica de la función $f$ se muestra a continuación. ¿Cuál parece ser el valor de  

​x→-2​lim​​           f(x) ?

 R//=lim x tiende a -6 después de analizarlo  por la izquierda y la derecha  es = 0

 R//=lim x tiende a -2 después de analizarlo  por la izquierda y la derecha  es = -3

- 2) La gráfica de una función $f$f se muestra a continuación. ¿Cuál es el límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $0$0?

-La gráfica de una función 

$f$f se muestra a continuación. ¿Cuál es el límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $0$2?02?

 R//=lim x tiende a 0 después de analizarlo  por la izquierda y la derecha  es = 3

 R//=lim x tiende a 2 después de analizarlo  por la izquierda y la derecha  es = 5

- 3) La gráfica de una función $f$f se muestra a continuación. ¿Cuál parece ser el valor límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $-8$minus, 8?

-La gráfica de una función 

$f$f se muestra a continuación. ¿Cuál parece ser el valor límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $-8$8?minus, 8?

 R//=lim x tiende a -8 después de analizarlo  por la izquierda y la derecha  es = -3

 R//=lim x tiende a 8 después de analizarlo  por la izquierda y la derecha  es = 6

- 4) La gráfica de una función $f$f se muestra a continuación. ¿Cuál parece ser el valor límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $-8$6?

-La gráfica de una función 

$f$f se muestra a continuación. ¿Cuál parece ser el valor límite de $f(x)$f, left parenthesis, x, right parenthesis a medida que $x$x se aproxima a $-8$9?

 R//=lim x tiende a 6 después de analizarlo  por la izquierda y la derecha  es = -1

 R//=lim x tiende a 9 después de analizarlo  por la izquierda y la derecha  es = 2

- 5) La gráfica de la función 

$f(x)=\sin x$f, left parenthesis, x, right parenthesis, equals, sine, x se muestra a continuación. ¿Cuál parece ser el valor límite de $\sin x$sine, x a medida que $x$x se aproxima a $\dfrac{\pi}{2}$π/2?

-La gráfica de la función 

$f(x)=\sin x$f, left parenthesis, x, right parenthesis, equals, sine, x se muestra a continuación. ¿Cuál parece ser el valor límite de $\sin x$sine, x a medida que $x$x se aproxima a $\dfrac{\pi}{2}$/2?

R//=lim x tiende a π/2  después de analizarlo  por la izquierda y la derecha  es = 1

R//=lim x tiende a 3/2  después de analizarlo  por la izquierda y la derecha  es = -1

start fraction, pi, divided by, 2, end fractio

minus, 8